Equation of a Line
A Linear Relation can be described using the equation of a line in slope-intercept form:
\(y = mx + b\)
Where \(m\) is the slope and \(b\) is the \(y\)-intercept.
The slope represents the steepness of the line while the \(y\)-intercept represents the point where the line crosses the \(y\)-axis.
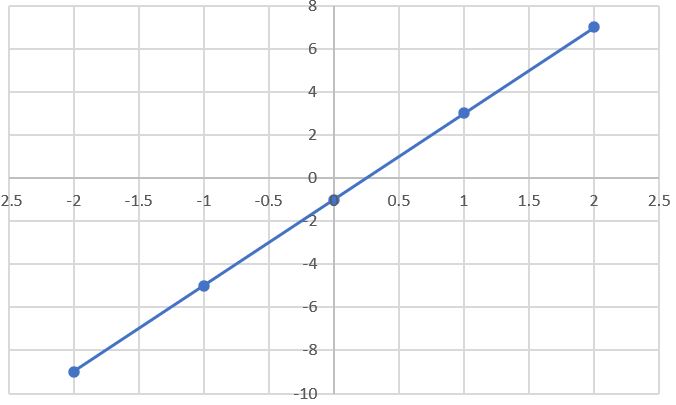
In the diagram below, the line crosses the \(y\)-axis at \(y=-1\) (y-intercept). Every time \(x\) increases by \(1\), \(y\) increases by \(4\) (slope). The equation of the line is:
\(y = 4x - 1\)
We can start by writing the equation of a line:
\(y = m(x) + b\)
Next, we will need the values of the slope, \(m\), and \(y\)-intercept, \(b\) to plug into the equation. From the question, we can identify both:
\( m = -2\)
\( b = \cfrac{1}{3}\)
Then, we can write our final equation:
\(\boldsymbol{y = -2x + \cfrac{1}{3}}\)
Other Forms
There are a few other ways we can write an equation of a line. One is the Point-Slope Form and another is Standard Form.
The equation for point-slope form is:
\(y - y_0 = m (x-x_0)\)
where \(m\) is the slope and \(x_0, y_0\) is a point on the line.
The equation for standard form is:
\(Ax + By = C\)
where \(A, B, C\) are coefficients wiht \(A, B \ne 0\).
You can convert an equation from Standard Form to Slope-Intercept Form or vice versa by rerranging the equation.
If we rearrange the equation for \(y\) we get:
\(y = \cfrac{-A}{B}x + \cfrac{C}{B}\)
From this equation, we can determine the slope as:
\(m = \cfrac{-A}{B}\)
Tyically, \(A, B, C\) are integers, \(A\) is positive and \(A, B, C\) do not share common factors.
Example
Convert \(x + 4y - 8 = 0\) to Point-Intercept Form.
First, we can isolate the term containing \(y\):
\(4y = -x + 8\)
Next, we can divide both sides by the coefficient of the \(y\)-term (\(4\)):
\(\cfrac{4y}{4} = \cfrac{-x + 8}{4}\)
\(y = \cfrac{-1x}{4} + {8}{4}\)
\(y = -\cfrac{1}{4}x + 2\)
Review these lessons:
Try these questions:
Y-intercept / X-intercept
Let's dig a little deeper into the y-intercept and the x-intercept.
Intercepts are points on a line where the line crosses the axes. The \(y\)-intercept is where the line crosses the \(y\)-axis. The \(x\)-intercept is where the line crosses the \(x\)-axis. See the figure below.
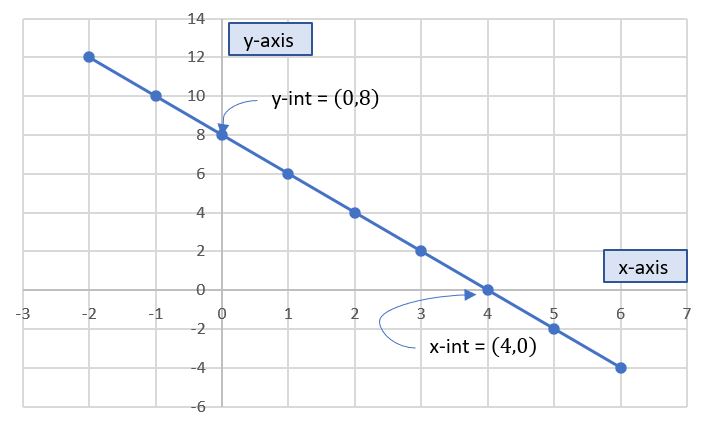
Notice that the \(x\)-value of the y-intercept and the \(y\)-value of the x-intercept are both \(0\). So, to solve for either intercept; we have to set the opposite value to zero.
Let's find the intercepts for the equation \(y = (-3)x - 4\).
| To find the x-intercept, set \(y = 0\). | To find the y-intercept, set \(x = 0\). |
|---|---|
| \(0 = -3(x) - 4\) | \(y = -3(0) - 4\) |
| To find the x-intercept, solve for \(x\). | To find the y-intercept, solve for \(y\). |
| \(4 = -3(x)\) | \(y = -4\) |
| \(x = \cfrac{-4}{3}\) | |
| x-intercept | y-intercept |
| \(\left(\cfrac{-4}{3},0\right)\) | \((0,-4)\) |
First, we can determine the \(y\)-intercept. We can set \( x=0 \) and solve for \(y\):
\( y = 12x - 24 \)
\( y = 12(0) - 24 \)
\( y = -24 \)
Next, we can determine the \(x\)-intercept. We can set \( y=0 \) and solve for \(x\):
\( y = 12x - 24 \)
\( 0 = 12x - 24 \)
\(12x = 24\)
\(\cfrac{\cancel{12}x}{\cancel{12}} = \cfrac{24}{12}\)
\(x = 2\)
Therefore, we can determine that the \(y\)-intercept is \(\boldsymbol{(0,-24)}\) and the \(x\)-intercept is \(\boldsymbol{(2,0)}\).