Binimial Therorem

Recall that a binomial is a polynomial with just two terms, typically written as \( a + b \). Expanding \((a+b)^n\) as \( n \) rises, the complexity grows. This lesson explains how to extend powers of binomials using Pascal's Triangle, a strategy that simplifies the procedure and is important in algebra and probability calculations.

Exploring Pascal's Triangle

Pascal's Formula represents a vital connection found in Pascal's Triangle, which is necessary for determining binomial coefficients. Each coefficient in the triangle is the sum of the two right above it, which makes difficult combinatorial computations easier.

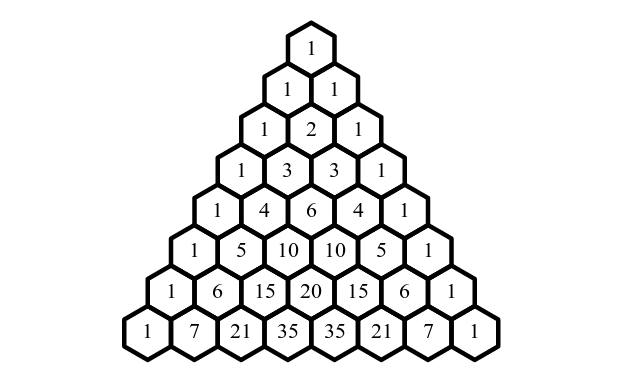
Pascal's Triangle is organized in a way that each number is the sum of the 2 numbers directly above it.

Note: It is important to note that \( t_{n,r} \) represents the term at the \(n\)th row and \(r\)th column of Pascal's Triangle, which is equal to \( C_{n,r}\), the binomial coefficient.

Pascal's Formula can be represented algebraically as such:

\(C_{n,r} = C_{n-1, r-1} + C_{n-1, r}\)

Where:

\(C_{n,r}\) represents the binomial coefficient
\(n\) represents the row number
\(r\) represents the column number

Proof of Pascal's Formula

This proof utilizes the factorial definition of the binomial coefficients, illustrating the systematic development of Pascal's Triangle:

\(C_{n,r} = \cfrac{n!}{r!(n-r)!}\) (Definition of binomial coefficient)

Using Pascal's relationship:

\(C_{n,r} = C_{n-1, r-1} + C_{n-1, r} \)

\(= \cfrac{(n-1)!}{(r-1)!(n-r)!} + \cfrac{(n-1)!}{r!(n-1-r)!} \)

Factorizing and simplifying:

\( = \cfrac{(n-1)!\cdot [r + (n - r)]}{r!(n-r)!} \)

\(= \cfrac{n!}{r!(n-r)!} \)

\(= C_{n,r} \)

This proof confirms that the binomial coefficient \( C_{n,r} \) can be derived by adding the coefficients \( C_{n-1, r-1} \) and \( C_{n-1, r} \), validating the recursive nature of Pascal’s Triangle.

Example

Compute the fourth entry in the fifth row of Pascal's Triangle.

First, we can identify \(n = 5\) and \(r = 4\).

Next, we can substitute these values into Pascal's Formula:

\(C_{n,r} = C_{n-1, r-1} + C_{n-1, r}\)

\(C_{5,4} = C_{5-1, 4-1} + C_{5-1, 4} \)

\(C_{5,4} = C_{4, 3} + C_{4, 4} \)

Then, we can calculate the respective coefficients using the following formula:

\(C_{n,r} = \cfrac{n!}{r!(n-r)!} \)

We can start by determining the first coefficient:

\(C_{4, 3} = \cfrac{4!}{3!(4-3)!} \)

\(C_{4, 3} = \cfrac{4 \times \cancel{3!}}{\cancel{3!}(1)!} \)

\(C_{4, 3} = \cfrac{4}{1} = 4\)

We can then determine the second coefficient:

\(C_{4, 4} = \cfrac{\cancel{4!}}{\cancel{4!}(4-4)!} \)

\(C_{4, 4} = \cfrac{1}{0!}\)

\(C_{4, 4} = \cfrac{1}{1} = 1\)

Finally, we can add the coefficients together to get the binomial coefficient:

\(C_{5,4} = C_{4, 3} + C_{4, 4}\)

\(C_{5,4} = 4 + 1\)

\(C_{5,4} = 5\)

Therefore, we can determine the fourth entry in the fifth row of Pascal's Triangle is 5.

This result aligns with Pascal's Triangle, confirming the effectiveness of Pascal’s Formula in practical scenarios. This example serves as a straightforward application to help students understand and utilize the formula in various combinatorial contexts.

Example

Use Pascal's Triangle to expand \((3x - 2y)^4\).

First, we can identify the coefficients from the 4th row of Pascal’s Triangle, which are 1, 4, 6, 4, 1.

Next, we can apply these coefficients to the binomial expansion:

\( (3x - 2y)^4 = 1(3x)^4 + 4(3x)^3(-2y) + 6(3x)^2(-2y)^2 + 4(3x)(-2y)^3 + 1(-2y)^4 \)

Then, we can calculate each term:

\( = (3x)^4 - 4 \cdot (3x)^3 \cdot 2y + 6 \cdot (3x)^2 \cdot 4y^2 - 4 \cdot 3x \cdot 8y^3 + 16y^4 \)

\( = 81x^4 - 72x^3y + 72x^2y^2 - 96xy^3 + 16y^4 \)

This gives the expanded form using the coefficients from Pascal’s Triangle.

To demonstrate the application of Pascal's formula in Pascal's Triangle, compute the sixth entry in the eighth row.

Show Answer

First, we can identify \(n = 8\) and \(r = 6\).

Next, we can substitute these values into Pascal's Formula:

\(C_{n,r} = C_{n-1, r-1} + C_{n-1, r}\)

\(C_{8,6} = C_{8-1, 6-1} + C_{8-1, 6}\)

\(C_{8,6} = C_{7, 5} + C_{7, 6}\)

Then, we can calculate the respective coefficients using the following formula:

\(C_{n,r} = \cfrac{n!}{r!(n-r)!}\)

We can start by determining the first coefficient:

\(C_{7,5} = \cfrac{7!}{5!(7-5)!}\)

\(C_{7,5} = \cfrac{7 \times 6 \times \cancel{5!}}{\cancel{5!}(2)!}\)

\(C_{7,5} = \cfrac{42}{2 \times 1}\)

\(C_{7,5} = \cfrac{42}{2} = 21\)

We can then determine the second coefficient:

\(C_{7,6} = \cfrac{7!}{6!(7-6)!}\)

\(C_{7,6} = \cfrac{7 \times \cancel{6!}}{\cancel{6!}(1)!}\)

\(C_{7,6} = \cfrac{7}{1} = 7\)

Finally, we can add the coefficients together to get the binomial coefficient:

\(C_{8,6} = C_{7, 5} + C_{7, 6}\)

\(C_{8,6} = 21 + 7\)

\(C_{8,6} = 28\)

Therefore, we can determine the sixth entry in the eighth row of Pascal's Triangle is 28.

Understanding the Binomial Theorem

The binomial theorem provides a method for expanding expressions that are raised to a power in the form \((a+b)^n\). This powerful theorem simplifies calculations that would otherwise be cumbersome, especially with larger powers.

We can express the binomial theorem algebraically as such:

\( (a + b)^n = C_n^0 a^n + C_n^1 a^{n-1}b + C_n^2 a^{n-2}b^2 + \dots + C_n^r a^{n-r}b^r + \dots + C_n^n b^n\)

\( (a + b)^n = \sum_{r=0}^{n} C_n^r a^{n-r}b^r \)

The coefficients in the \( (a + b)^n \) expansion correspond to the terms in row n of Pascal's triangle.

Example

Expand \((x + 2)^4\) using the Binomial Theorem.

Using the binomial theorem, we can calculate each term using the following formula:

\((x + 2)^4 = \sum_{r=0}^{4} C_4^r x^{4-r} 2^r\)

Next, we can calculate each term as such:

\(C_4^0 x^4 \cdot 2^0 = 1 \cdot x^4 \cdot 1 = x^4\)

\(C_4^1 x^3 \cdot 2^1 = 4 \cdot x^3 \cdot 2 = 8x^3\)

\(C_4^2 x^2 \cdot 2^2 = 6 \cdot x^2 \cdot 4 = 24x^2\)

\(C_4^3 x^1 \cdot 2^3 = 4 \cdot x \cdot 8 = 32x\)

\(C_4^4 x^0 \cdot 2^4 = 1 \cdot 1 \cdot 16 = 16\)

Then, we can find the sum of all terms:

\((x + 2)^4 = x^4 + 8x^3 + 24x^2 + 32x + 16\)

Therefore, we can determine that \((x + 2)^4 \) expanded is x⁴ + 8x³ + 24x² + 32x + 16.

Find the coefficient of \(x^5 \) in the expansion of \((3x - 2)^7\).

Show Answer

First, we can determine the general term in the binomial expansion of \((3x - 2)^7\) is given by \(\dbinom{7}{k} (3x)^{7-k}(-2)^k\).

Since we want the term with \(x^5\), we can set \(7 - k = 5\). We can then solve for \(k\) as such:

\(k = 7 - 5\)

\(k = 2\)

We can now identify the term with \(x^5\) is \(\dbinom{7}{2}(3x^{7-2})(-2)^2\).

Next, we can calculate the binomial coefficient by substituting the pertinent values into Pascal's formula and solving. From what we determined above, we can identify \(n = 7\) and \(r = 2\):

\(C_{7,2} = \cfrac{n!}{r!(n-r)!}\)

\(= \cfrac{7!}{2!(7-2)!}\)

\(= \cfrac{7\times 6 \times \cancel{5!}}{2!\cancel{5!}}\)

\(= \cfrac{7\times 6}{2 \times 1}\)

\(= \cfrac{42}{2} = 21\)

Then, we can calculate the term as such:

\(= 21(3x)^5(-2)^2\)

\(= 21(243x^5)(4)\)

\(= 20412x^5\)

Therefore, we can determine the coefficient of \(x^5\) in the expansion of \((3x - 2)^7\) is 20,412.