Pascal's Triangle
Pascal's Triangle is the arrangement of coefficients that can be used to determine the coefficients of Binomial Expansion. It has various practical applications in areas such as probability and algebra.
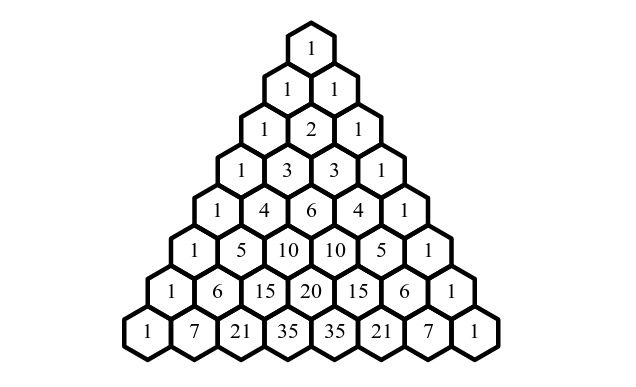
When building the Pascal's Triangle, we need to consider a couple of things:
- The values of the first and last cells on each row are 1
- The value of any other cell(s) can be determined by summing the 2 values of the cells directly above it
The pattern in each row of the Pascal's Triangle can be expressed algebraically as:
When determining the simplified result for a binomial expression, we can use binomial expansion (also known as FOIL) then collect like terms if possible.
The sum of values on each row can be expressed algebraically as \(2^n\).
The # of elements in each row can be expressed algebraically as:
In each of these formulas, \(n\) represents the row # with n starting at 0.
Note: Each binomial expression you encounter may use completely different terms. They might use different sets of letters (i.e. \(a\) and \(b\) instead of \(x\) and \(y\)) or numbers rather than letters.
Example
Expand and simplify each binomial:
- \((a + b)²\)
- \((m + n)⁴\)
i. We can first use simple binomial expansion to expand the expression:
\(= (\textcolor{red}{a} + \textcolor{green}{b})\textcolor{blue}{²}\)
\(= (\textcolor{red}{a} + \textcolor{green}{b})(\textcolor{red}{a} + \textcolor{green}{b})\)
\(= (\textcolor{red}{a})(\textcolor{red}{a}) + (\textcolor{red}{a})(\textcolor{green}{b}) + (\textcolor{green}{b})(\textcolor{red}{a}) + (\textcolor{green}{b})(\textcolor{green}{b})\)
Now that our expression is expanded, we can simplify further by collecting like terms:
\(= \textcolor{red}{a²} + \textcolor{red}{a}\textcolor{green}{b} + \textcolor{red}{a}\textcolor{green}{b} + \textcolor{green}{b²}\)
\(= 1a² + 2ab + 1b²\)
Therefore, we can determine that \((a + b)²\) expanded and simplified is 1a² + 2ab + 1b². This makes sense when comparing it to Pascal's Triangle since the expressions coefficients match the Triangle's values on the second row, 1 2 1.
ii. We will use the same process as the question above. The result will be more complicated since we are dealing with more terms. We can start by expanding the expression in 2 sets of brackets:
\(= (\textcolor{red}{m} + \textcolor{green}{n})⁴\)
\(= (\textcolor{red}{m} + \textcolor{green}{n})(\textcolor{red}{m} + \textcolor{green}{n})(\textcolor{red}{m} + \textcolor{green}{n})(\textcolor{red}{m} + \textcolor{green}{n})\)
\(= [(\textcolor{red}{m})(\textcolor{red}{m}) + (\textcolor{red}{m})(\textcolor{green}{n}) + (\textcolor{green}{n})(\textcolor{red}{m}) + (\textcolor{green}{n})(\textcolor{green}{n})][(\textcolor{red}{m})(\textcolor{red}{m}) + (\textcolor{red}{m})(\textcolor{green}{n}) + (\textcolor{green}{n})(\textcolor{red}{m}) + (\textcolor{green}{n})(\textcolor{green}{n})]\)
We can now simplify the expression by collecting like terms in each bracket. After, we can expand the expression further:
\(= [\textcolor{red}{m²} + \textcolor{red}{m}\textcolor{green}{n} + \textcolor{red}{m}\textcolor{green}{n} + \textcolor{green}{n²}][\textcolor{red}{m²} + \textcolor{red}{m}\textcolor{green}{n} + \textcolor{red}{m}\textcolor{green}{n} + \textcolor{green}{n²}]\)
\(= [\textcolor{red}{m²} + 2\textcolor{red}{m}\textcolor{green}{n} + \textcolor{green}{n²}][\textcolor{red}{m²} + 2\textcolor{red}{m}\textcolor{green}{n} + \textcolor{green}{n²}]\)
\(= [m² + 2mn + n²][m² + 2mn + n²]\)
Now we expand again:
\(= [\textcolor{orange}{m²} + 2\textcolor{blue}{mn} + \textcolor{purple}{n²}][\textcolor{orange}{m²} + 2\textcolor{blue}{mn} + \textcolor{purple}{n²}]\)
\(= (\textcolor{orange}{m²})(\textcolor{orange}{m²}) + (\textcolor{orange}{m²})(2\textcolor{blue}{mn}) + (\textcolor{orange}{m²})(\textcolor{purple}{n²}) + (2\textcolor{blue}{mn})(\textcolor{orange}{m²}) + (2\textcolor{blue}{mn})(2\textcolor{blue}{mn}) + (2\textcolor{blue}{mn})(\textcolor{purple}{n²}) + (\textcolor{purple}{n²})(\textcolor{orange}{m²}) + (\textcolor{purple}{n²})(2\textcolor{blue}{mn}) + (\textcolor{purple}{n²})(\textcolor{purple}{n²})\)
We can simplify the expression further by collecting more like terms:
\(= m^4 + 2m^3n + m^2n^2 + 2m^3n + 4m^2n^2 + 2mn^3 + n^2m^2 + 2n^3m + 1n^4\)
\(= \textcolor{green}{m^4} + \textcolor{orange}{2m^3n} + \textcolor{blue}{m^2n^2} + \textcolor{orange}{2m^3n} + \textcolor{blue}{4m^2n^2} + \textcolor{red}{2mn^3} + \textcolor{blue}{n^2m^2} + \textcolor{red}{2n^3m} + \textcolor{purple}{1n^4}\)
\(= \textcolor{green}{m⁴} + \textcolor{orange}{4m³n} + \textcolor{blue}{6m²n²} + \textcolor{red}{4mn³} + \textcolor{purple}{n⁴}\)
Therefore, we can determine that \((m + n)⁴\) expanded and simplified is 1m⁴ + 4m³n + 6m²n² + 4mn³ + 1n⁴. When comparing it to Pascal's Triangle since the expressions coefficients match the Triangle's values on the fourth row, 1 4 6 4 1.
\((x + y)^3\)
Using the 4th row, we get the following:
\((a - b)^4\)
Using the 5th row, we get the following:
\((2x + 1)^5\)
We can use Pascal's Triangle to expand and simplify the binomial expression. We will multiply these terms by the coefficients on Row 5:
\(= (\textcolor{red}{2x} + \textcolor{green}{1})\textcolor{blue}{⁵}\)
\(= 1(\textcolor{red}{2x})\textcolor{blue}{⁵}(\textcolor{green}{1})\textcolor{magenta}{⁰} + 5(\textcolor{red}{2x})\textcolor{blue}{⁴}(\textcolor{green}{1})\textcolor{magenta}{¹} + 10(\textcolor{red}{2x})\textcolor{blue}{³}(\textcolor{green}{1})\textcolor{magenta}{²} + 10(\textcolor{red}{2x})\textcolor{blue}{²}(\textcolor{green}{1})\textcolor{magenta}{³} + 5(\textcolor{red}{2x})\textcolor{blue}{¹}(\textcolor{green}{1})\textcolor{magenta}{⁴} + 1(\textcolor{red}{2x})\textcolor{blue}{⁰}(\textcolor{green}{1})\textcolor{magenta}{⁵}\)
\(= 32x⁵ + 80x⁴ + 80x³ + 40x² + 10x + 1\)
Therefore, we can determine that \((2x + 1)⁵\) expanded and simplified is 32x⁵ + 80x⁴ + 80x³ + 40x² + 10x + 1.
\((\sqrt{m}- 3)^6\)
We can use Pascal's Triangle to expand and simplify the binomial expression. We will multiply these terms by the coefficients on Row 6:
\((\textcolor{red}{\sqrt{m}} - \textcolor{green}{3})\textcolor{blue}{⁶}\)
\(= 1(\textcolor{red}{\sqrt{m}})\textcolor{blue}{⁶}(\textcolor{green}{-3})\textcolor{magenta}{⁰} + 6(\textcolor{red}{\sqrt{m}})\textcolor{blue}{⁵}(-3)\textcolor{magenta}{¹} + 15(\textcolor{red}{\sqrt{m}})\textcolor{blue}{⁴}(\textcolor{green}{-3})\textcolor{magneta}{²} + 20(\textcolor{red}{\sqrt{m}})\textcolor{blue}{³}(\textcolor{green}{-3})\textcolor{magenta}{³} + 15(\textcolor{red}{\sqrt{m}})\textcolor{blue}{²}(\textcolor{green}{-3})\textcolor{magenta}{⁴} + 6(\textcolor{red}{\sqrt{m}})\textcolor{blue}{¹}(\textcolor{green}{-3})\textcolor{magenta}{⁵} + 1(\textcolor{red}{\sqrt{m}})\textcolor{blue}{⁰}(\textcolor{green}{-3})\textcolor{magenta}{⁶}\)
\(= (1)(\textcolor{red}{m^{\frac{1}{2}}})\textcolor{blue}{⁶} + (6)(\textcolor{green}{-3})(\textcolor{red}{m^{\frac{1}{2}}})\textcolor{blue}{⁵} + (15)(\textcolor{green}{9})(\textcolor{red}{m^{\frac{1}{2}}})\textcolor{blue}{⁴} + (20)(\textcolor{green}{-27})(\textcolor{red}{m^{\frac{1}{2}}})\textcolor{blue}{³} + (15)(\textcolor{green}{81})(\textcolor{red}{m^{\frac{1}{2}}})\textcolor{blue}{²} + (6)(\textcolor{green}{-243})(\textcolor{red}{m^{\frac{1}{2}}})\textcolor{blue}{¹} + 729\)
\(= 1m^{3} - 18m^{\frac{5}{2}} + 135m^{2} - 540m^{\frac{3}{2}} + 1215m - 1458m^{\frac{1}{2}} + 729\)
Therefore, we can determine that \((\sqrt{m}- 3)⁶\) expanded and simplified is 1m3 - 18m5/2 + 135m2 - 540m3/2 + 1215m - 1458m1/2 + 729.
Pascal's Triangle and Combinations
Each number in Pascal's Triangle represents a binomial coefficient, which is the number of ways to choose \(r\) items from a set of \(n\) items:
The Combination Formula is:
Where Row \(n\) of Pascal's Triangle contains the values:
We use the combination formula to find how many ways we can choose 3 members from 8:
\(\dbinom{8}{3} = \cfrac{8!}{3!(8-3)!}\)
\(\dbinom{8}{3} = \cfrac{8!}{3!5!}\)
\(\dbinom{8}{3} = \cfrac{8 \times 7 \times 6}{3 \times 2 \times 1}\)
\(\dbinom{8}{3} = 56\)
Therefore, 56 unique combinations of 3 members can be chosen from 8 candidates.