1. Lessons
  2. Gr12
  3. Math
  4. Data Management
  5. Applying Pascal's Method

Applying Pascal's Method

Pascal's Triangle is a powerful tool in combinatorics, probability, and algebra. In this lesson, we will apply Pascal's Method to solve various practice questions and word problems that involve binomial expansion, counting paths, and probability.

Practice Questions

Using Pascal's Triangle, determine the value of the following:

\( \binom{6}{2} \)

We

Using Pascal's Triangle, we get the following:

\(\binom{6}{2} = \cfrac{6!}{2!(6-2)!}\)

\(= \cfrac{6!}{2!4!}\)

\(= \cfrac{6 \times 5}{2 \times 1}\)

\(= 15\)

Therefore, we can determine the value using Pascal's Triangle is 15.

\(\binom{8}{3} \)

The sum of the elements in row 6 of Pascal's Triangle.

Using Pascal's Triangle, we get the following:

\[ \binom{8}{3} = \frac{8!}{3!(8-3)!} = \frac{8!}{3!5!} = \frac{8 \times 7 \times 6}{3 \times 2 \times 1} = 56 \]

Therefore, we can determine the value using Pascal's Triangle is 56.

Pascal's Triangle row 6: 1, 5, 10, 10, 5, 1

\(1 + 5 + 10 + 10 + 5 + 1 = 32\)

Therefore, we can determine the sum of elements in row 5 of Pascal's Triangle is 32.

Binomial Expansion using Pascal's Triangle

Using Pascal's Triangle, determine the value of the following:

\((x + y)^3\)

Using the 4th row, we get:

\[(x + y)^3 = 1x^3 + 3x^2y + 3xy^2 + 1y^3\]

\( (a - b)^4 \)

Using the 4th row, we get:

\[(x + y)^3 = 1x^3 + 3x^2y + 3xy^2 + 1y^3\]

Word Problems

In a family tree, each generation doubles in size. Suppose a person is at generation 0. Their parents are in generation 1, grandparents in generation 2, and so on. How many ancestors does this person have in generation 5?

We can determine the answer by using Pascal's Triangle. Looking at row 5 of Pascal's Triangle:

\(1,5,10,10,5,1\)

So, the total number of generations is:

\(1+5+10+10+5+1 = 32\)

Therefore, we can determine that by generation 5 there will be 32 ancestors.

A pyramid-shaped array of letters is formed as follows:

A person starts at the top letter C and moves downward, choosing to step diagonally left or right at each level. How many unique paths spell the word CODE?

Starting at the top, record the number of possible paths moving diagonally to the left and right as you proceed to each different letter. By following Pascal's Triangle's path-counting method, we can develop the following path:

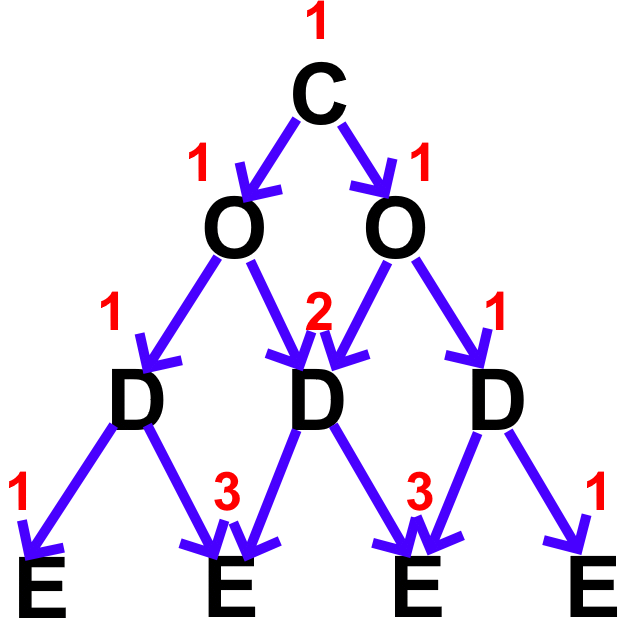
Each letter's value is the sum of the two paths leading to it. Assigning values from Pascal's Triangle, the number of paths leading to each E is 6.

Therefore, Summing the paths at the last row gives us:

\(1 + 3 + 3 + 1 = 8\)

Therefore, we can determine there are 8 unique paths that can spell the word CODE.