Reciprocal Trigonometric Functions
Reciprocal Trigonometric Functions consist of \(3\) algebraic functions that incorporate reciprocal trigonometric ratios. The main trigonometric functions are cosecant, secant, and cotangent. They are related to the graphs of the primary trigonometric functions as reciprocal graphs. They can be expressed algebraically as such:
Reciprocal trigonometric functions, like the primary trigonometric functions, are periodic since they repeat themselves at regular intervals.
Reciprocal functions are different from inverse trigonometric functions; for instance, \(\csc x\) also represents \(\cfrac{1}{\sin(x)}\) whereas \(\sin^{-1}\) asks you to find an angle that has a sine ratio equal to \(x\).
Types of Reciprocal Trigonometric Functions
Cosecant Functions
Cosecant Functions are trigonometric functions that can be expressed algebraically as:
They are represented graphically as:
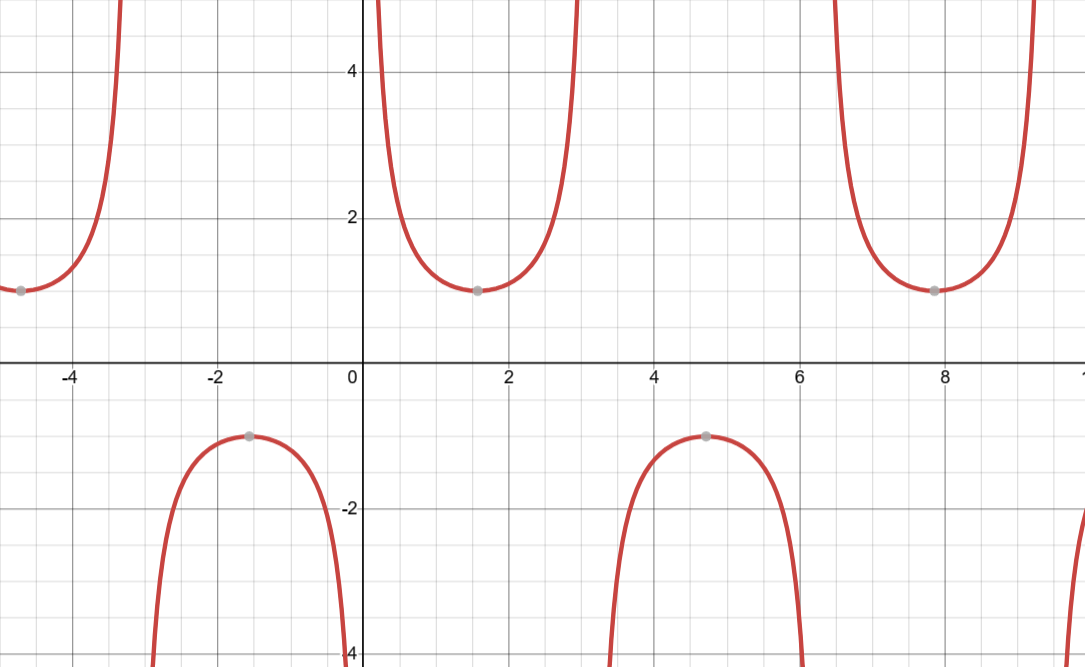
Graphically, we can identify that the vertical asymptotes of cosecant function match the locations of the sine function’s x-intercepts, which are in intervals of \(\pi\). Likewise, the extrema of the cosecant function’s pieces are the same as the opposite extrema of the sine function (i.e., a max of the sine function represents the min of a cosecant function since taking the reciprocal of a big number results in a smaller one).
The Period of a cosecant function is \(2\pi\) rads.
The Domain can be expressed as x is an element of all real numbers that aren’t multiples of \(\pi\) or \(\{x\in\mathbb{R} | x \ne \pi n\)}.
The Range can be expressed as \(y\) is an element of all real numbers that are either equal or greater than \(1\) or equal or less than \(-1\) or \(\{y \in \mathbb{R} |y \ge 1, y \le -1\}\).
Secant Functions
Secant Functions are trigonometric functions that can be expressed algebraically as:
They are represented graphically as:
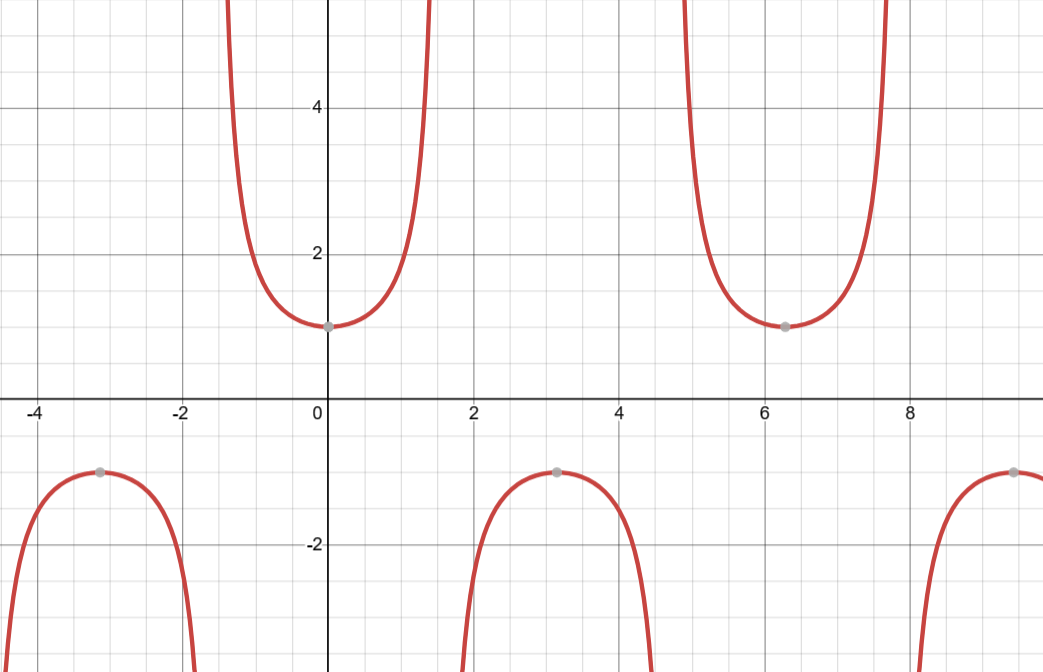
Graphically, we can identify that the Vertical Asymptotes of secant function match the locations of the cos function’s x-intercepts, which are in odd intervals of \(π/2\). Likewise, the extrema of the cosecant function’s pieces are the same as the opposite extrema of the sine function (i.e., a max of the sine function represents the min of a cosecant function since taking the reciprocal of a big number results in a smaller one).
The Period of a cosecant function is \(2π\) rads.
The Domain can be expressed as x is an element of all real numbers that aren’t multiples of \(\pi\) or \(\{x\in\mathbb{R} | x \ne \cfrac{\pi}{2}(2n+1)\)}.
The Range can be expressed as \(y\) is an element of all real numbers that are either equal or greater than \(1\) or equal or less than \(-1\) or {\(y\in\mathbb{R} |y \ge 1, y \le -1\)}.
Cotangent Functions
Cotangent Functions are trigonometric functions that can be expressed algebraically as:
They are represented graphically as:

Graphically, we can identify that the Vertical Asymptotes of cotangent function match the locations of the tan function’s x-intercepts and vice versa. The vertical asymptotes of the cotangent function are located in intervals of . The respective pieces of the tangent and cotangent functions also cross over each other in between each asymptote.
The Period of a cosecant function is \(\pi\) rads.
The Domain can be expressed as \(x\) is an element of all real numbers that aren’t multiples of \(\pi\) or \(\{x\in\mathbb{R} | x \ne \pi n\}\).
The Range can be expressed as y is an element of all real numbers or \(\{y\in\mathbb{R}\}\).