Volume
The Volume of an 3D object is the total quantity of space the shape occupies. The volume of an object is measured in cubic units such as cubic centimeters, cubic inch, cubic foot, cubic meter, etc. Finding the volume of an object can help us to determine the amount required to fill that object like the amount of water needed to fill a bottle, an aquarium or a water tank.
Volume of Common Shapes
Cube

The volume of a cube with length \(s\) is calculated by:
\(V = s^3\)
Cuboid

The volume of a cuboid (rectangular prism) with length \(l\), width \(w\) and height \(h\) is calculated by:
\(V = l w h\)
Cone
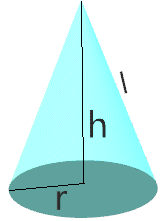
The volume of a cone with height \(h\), slant \(l\) and radius \(r\) is calculated by:
\(V = \cfrac{1}{3} \pi r^2 h\)
Cylinder

The volume of a cylinder with radius \(r\) and height \(h\) is calculated by:
\(V = \pi r^2 h\)
Triangular Prism

The volume of a triangular prism with two equal side lengths \(s\), base \(b\), height \(h\), and length \(l\) is calculated by:
\(V = \cfrac{1}{2} b h l\)
Sphere
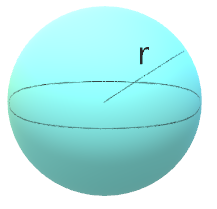
The volume of a sphere with radius \(r\) is calculated as:
\(V = \cfrac{4}{3} \pi r^3\)
Note that the volume of shapes like prisms and cylinders can be calculated as:
\( V = A_{\text{base}}h \)
ExampleFind the volume of a pentagonal prism with a base Area of \(12 \; [\text{cm}^2]\) and a height of \(20 \; [\text{cm}]\).
In order to determine the volume of the pentagonal prism, we can plug the appropriate values into the formula listed above and simplify:
\(V = A_{\text{base}}h \)
\(V = (12)(20) \)
\(V = 240 \; [\text{cm}^3]\)
Therefore, we can determine the volume of the pentagonal prism is \(\boldsymbol{240 \; [\textbf{cm}^3]}\).
First, we can convert the boxes side length from centimeters to meters:
\(\text{Side Length} = 50 \; [\cancel{\text{cm}}] \times \cfrac{1 \; [\text{m}]}{100 \; [\cancel{\text{cm}}]}\)
\(\text{Side Length} = 0.50 \; [\text{m}]\)
The volume of a rectangle prism is calculated by plugging values into the cuboid formula and simplifying:
\(V = l w h \)
\(V_{\text{box}} = (0.50) (0.50) (0.50)\)
\(V_{\text{box}} = 0.125 \; [\text{m}^3]\)
Since there are \(18\) boxes inside the crate, we can determine the total volume of the crate as such:
\(V_{\text{crate}} = 18 *(0.125)\)
\(V_{\text{crate}} = 2.25 \; [\text{m}^3] \)
The volume of the crate is \(\boldsymbol{2.25 \; [\textbf{m}^3]}\).
In order to determine the radius of the sphere, we substitute the appropriate values into the corresponding formula and simplify:
\(V = \cfrac{4}{3} \pi r^3\)
\(320 = \cfrac{4}{3} \pi r^3\)
\(\cfrac{3}{4\pi}(320) = \cancel{\cfrac{3}{4 \pi}}\left(\cancel{\cfrac{4}{3}} \cancel{\pi} r^3\right)\)
\(76.39 = r^3\)
\(\sqrt[3]{76.39} = \sqrt[3]{r^3}\)
\(r \approx 4.2 \; [\text{m}]\)
Therefore, we can determine that the radius of the sphere is approximately \(\boldsymbol{4.2 \; [\textbf{m}]}\).
We can determine the volume of the soda can by plugging the appropriate values into the cylinder formula:
\(V = \pi r^2 h\)
\(V = \pi (4)^2 (13)\)
\(V_{\text{soda can}} = 653.45 \; [\text{cm}^3]\)
Therefore, we can detemrmine that the volume of the soda can is \(\boldsymbol{653.45 \; [\textbf{cm}^3]}\)
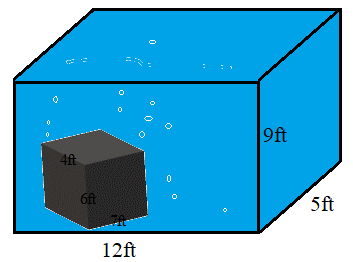
To calculate the volume of water, we need to calculate the volume of the water tank and subtract the volume of the metal box. This is because the metal block displaces the water in the tank as it occupies some volume.
The volume of a rectangle prism is calculated by plugging values into the cuboid formula and simplifying:
\(V = l w h \)
First, we can determine the volume of the tank:
\(V_{\text{tank}} = (12)(5)(9)\)
\(V_{\text{tank}} = 540 \; [\text{ft}^3]\)
Next, we can determine the volume of the metal box:
\(V_{\text{box}} = (7)(4)(6)\)
\(V_{\text{box}} = 168 \; [\text{ft}^3]\)
Finally, we can determine the volume of water left in the tank by calculating the difference between the tank and metal box:
\(V_{\text{water}} = V_{\text{tank}} - V_{\text{water}}\)
\(V_{\text{water}} = 540 - 168\)
\(V_{\text{water}} = 372 \; [\text{ft}^3]\)
Therefore, we can determine the volume of water left in the tank is \(\boldsymbol{372 \; [\textbf{ft}^3]}\).
In order to determine how much oil the funnel can hold, we first need to identify the funnel's height. We can find this value using the Pythagorean theorem:
\(s^2 = h^2 + r^2\)
\((9.2)^2 = h^2 + (4.8)^2\)
\(84.64 = h^2 + 23.04\)
\(h^2 = 84.64 - 23.04\)
\(h^2 = 61.6\)
\(\sqrt{h^2} = \sqrt{61.6}\)
\(h = 7.85 \; [\text{cm}]\)
Next, we can use the cone's corresponding volume formula to determine how much oil the funnel can hold:
\(V = \cfrac{1}{3} \pi r^2 h\)
\(V = \cfrac{1}{3} \pi (4.8)^2(7.85)\)
\(V = \cfrac{1}{3} (24.66) (23.04)\)
\(V = \cfrac{1}{3}(568.20)\)
\(V = 189.4 \; [\text{cm}^3]\)
Therefore, we can determine that the funnel can hold \(\boldsymbol{189.4 \; [\textbf{cm}^3]}\) of oil.