Perimeter
The Perimeter of a 2D shape, such as square, rectangle or triangle, is the sum of all the sides of the shape. For a circle, the perimeter is the length of the boundary of the circle called the Circumference.
Perimeter of Common Shapes
Let's look at how to calculate the perimeter of the shapes below:
Triangle
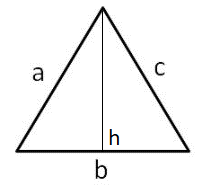
The perimeter of a triangle with side lengths \(a\), \(b\) and \(c\) is calculated as:
\(P = a + b + c\)
Square

The perimeter of a square with side length \(s\) is calculated as:
\(P = 4s\)
Rectangle

The perimeter of a rectangle with side lengths \(l\) and \(w\) is calculated as:
\(P = 2l + 2w\)
Circle
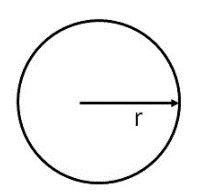
The perimeter of a circle with radius \(r\) is calculated as:
\(P = 2 \pi r\)
Trapezoid

The perimeter of a trapezoid with side lengths \(a\), \(b\), \(c\), and \(d\) is calculated as:
\(P = a + b + c + d\)
Parallelogram
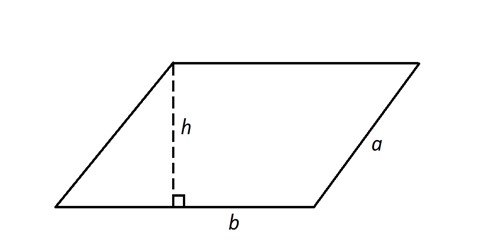
The perimeter of a parallelogram with side lengths \(a\) and \(b\) is calculated as:
\(P = 2a + 2b\)
An isosceles triangle has two equal lengths. The other length is known.
First, we can rewrite the formula for the perimeter of a triangle:
\(P = a + b + c\)
Since we are looking at an isoceles triangle, this means that \(2\) side lengths are the same; as a result, we can change \(c\) to another \(b\):
\(P = a + b + b\)
Next, we can plug in the known values and collect like terms:
\(44 = 10 + b + b\)
\(34 = 2b\)
Finally, we can solve for \(b\) by dividing both sides by \(2\):
\(\cfrac{\cancel{2}b}{\cancel{2}} = \cfrac{34}{2}\)
\(b = 17 \; [\text{m}]\)
Therefore, we can determine that the length of the other \(2\) sides are both \(\boldsymbol{17 \; [\textbf{m}]}\).

First, we can determine the perimeter of the semi-circle is half the perimeter of the full circle plus the diameter. This can be expressed as such:
\(P = \cfrac{1}{2} 2\pi r + 2r\)
Since we know the diameter, we can determine the radius by dividing it by \(2\):
\(r = \cfrac{d}{2} = \cfrac{43}{2} = 21.5 \; [\text{cm}]\)
Finally, we can plug the value of the radius into the original formula and solve for the perimeter:
\(P = \cfrac{1}{2} 2\pi (21.5) + 2(21.5) \)
\(P = 110.54 \; [\text{cm}]\)
Therefore, we can determine that the perimeter of the semi-circle is \(\boldsymbol{110.54 \; [\textbf{cm}]}\).
First, we need to find the perimeter of the clock using the formula of a circle:
\(P_{\text{Clock}} = 2 \pi r\)
\(P_{\text{Clock}} = 2 \pi (20) \)
\(P_{\text{Clock}} = 125.6 \; [\text{cm}]\)
Next, we can determine the total distance the second hand's arrow travelled. Since the second hand spun around the clock \(3\) times, that meant it traveled \(3\) times the length of the perimeter:
\(P_{\text{Total}} = (125.6)(3)\)
\(P_{\text{Total}} = 376.8 \; [\text{cm}]\)
Therefore, we can determine that the second hand travelled \(\boldsymbol{376.8 \; [\textbf{cm}]}\) in total during \(3\) full rotations around the clock.