Surface Area

The Surface Area of a 3D shape is the sum of the areas of each face. Surface area is also measured in square units such as square centimeters ( $\text{cm}^2$ ), square inches ( $\text{in}^2$ ) etc.

Surface Area of Common Shapes

Let's look at how to calculate the surface area of the shapes below:

Cube

The surface area of a cube with side length $s$ is calculated as:

$SA = 6 s^2$

Cuboid

The surface area of a cuboid (rectangular prism) with length $l$, width $w$ and height $h$ is calculated as:

$SA = 2 (l w + l h + w h)$

Cone

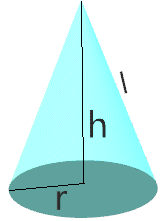
The surface area of a cone with height $h$, slant $l$, and radius $r$ is calculated as:

$SA = \pi r (l + r)$

Cylinder

The surface area of a cylinder with radius $r$ and height $h$ is calculated as:

$SA = 2 \pi r (h + r)$

Triangular Prism

The surface area of a triangular prism with two equal side lengths $s$, base $b$, height $h$ and length $l$ is calculated as:

$SA = bh + 2ls + lb$

Sphere

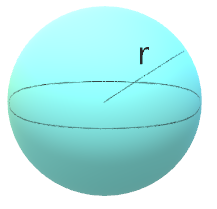
The surface area of a sphere with radius $r$ is calculated as:

$SA = 4 \pi r^2 $

Surface Area Using Nets

The net of an 3D shape is formed when the shape is unfolded along its edges and its faces are laid out in a pattern in 2D. Nets are helpful to visualize the different faces of a 3D object to calculate the surface area.

Let's draw a net for the shape below.

Cuboid with a height of 6cm, length of 3cm, and width of 2cm.

We have to unfold the 3D object to get the net shape below:

Net shape of a cuboid with height of 6cm, length of 3cm, and width of 2cm.

You can see that the original 3D shape is made up of $6$ rectangles. We can calculate the area of each using $A = lw$. Lastly, we add them all up to get the surface area.

$SA = (2)(6) + (3)(6) + (2)(6) + (3)(6) + (3)(2) + (3)(2) $

$SA = 2 ( (2)(6) + (3)(6) + (3)(2) )$

$SA = 2 (12 + 18 + 6)$

$SA = 72 \; [\text{cm}^2]$

Therefore, we can determine that the surface area is $\boldsymbol{72 \; [\textbf{cm}^2]}$.

A sphere has a radius $6$ inches. What is its surface area?

Show Answer

In order to determine the surface area of a sphere, we can plug its radius into its corresponding formula and solve:

$SA = 4 \pi r^2 $

$SA = 4 \pi (6)^2 $

$SA = 452.39 \; [\text{in}^2]$

Therefore, we can determine that the surface area of the sphere is $\boldsymbol{452.39 \; [\textbf{in}^2]}$.

The lateral area of a cone with radius $3\; [\text{cm}]$ is $72\; [\text{cm}^2]$. Determine the slant height of the cone, to the nearest centimetre.

Show Answer

In order to determine the slant height of the cone, we can first substitute the appropriate values into its corresponding surface area formula:

$SA = \pi r (l + r)$

$72 = \pi \cdot 3 (l + 3)$

Next, we can expand the equation and rearrange it:

$72 = \pi (3l + 9)$

$72 = 9.425l + 28.275$

$9.425l = 72 - 28.275$

We can now simplify:

$9.425l = 43.725$

$\cfrac{\cancel{9.425}l}{\cancel{9.425}} = \cfrac{43.725}{9.425}$

$l \approx 5\; [\text{cm}]$

Therefore, we can determine that the slant height of the cone, to the nearest centimetre, is $\boldsymbol{5\; [\textbf{cm}]}$.

Juan is making a yard sign in the shape of a rectangular prism. The yard sign will be $60 \; [\text{cm}]$ long, $40 \; [{\text{cm}}]$ high and $5 \; [\text{cm}]$ thick. The cost of painting the yard sign is $$0.002$ per square $\text{cm}$. How much does Juan have to spend to paint the yard sign?

Show Answer

First, we can determine the surface area of the sign. The surface area of a rectangular prism (which the sign represents) is calculated by adding the area of all $6$ sides of prism. We can plug in the appropriate values to solve:

$SA = 2 (l w + l h + w h)$

$SA = 2 ((60)(5) + (60)(40) + (5)(40)) $

$SA = 2 (300 + 2400 + 200)$

$SA = 2 (2900)$

$SA = 5800 \; [\text{cm}^2]$

Next, we can calculate the cost of painting by multiplying the surface area by the rate since Juan will need to paint all sides of the sign.

$C = SA \cdot r$

$C = 5800 \; \cancel{\text{cm}^2} \cdot \cfrac{$0.002}{\cancel{\text{cm}^2}}$

$C = $11.60$

Therefore, we can determine that it will cost $\boldsymbol{$11.60}$ to paint the sign.

Draw a net for the shape below and calculate the surface area.

Cylinder with a diameter of 4cm and a height of 10cm.

Show Answer

First, we can draw the net:

A net of a cylinder with a diameter of 4cm and a height of 10cm.

The top and bottom of the cylinder are circles. The middle portion will unfold to a rectangle. The width of the rectanle is the circiumference of the circle! Recall the circiumference of a circle is $\pi d = 2 \pi r$.

The Surface Area of a cylinder consists of $2$ circles plus a rectangle:

$SA = 2 \pi r^2 + 2 \pi r h$

Next, we can determine the circle's radius, which is half its diameter:

$r = \cfrac{d}{2} = \cfrac{4}{2} = 2\; [\text{cm}]$

Then, we can use the formula below (which is a simplifed version), to determine the surface area of the cylinder:

$SA = 2 \pi r (h + r)$

$SA = 2 \pi 2(10 + 2)$

$SA = 4 \pi (12)$

$SA = 150.80 \; [\text{cm}^2]$

Therefore, we can determine that the surface area of the cylinder is $\boldsymbol{150.80 \; [\textbf{cm}^2]}$.

Review these lessons:

Try these questions:

Take the Quiz:

Sufrace Area