The Iterative Process
The iterative process involves repeating a set of steps over and over to solve a problem or complete a task. Each repetition (or iteration) brings us closer to the final solution.
Iterations
An iteration is one complete cycle of repeating the same set of steps in a process. In Data Management, iterations are used to improve and refine processes.
Example: When practicing a dance routine, you repeat the steps over and over to get better each time. Each time you practice, you improve and refine your moves.
Algorithms
An algorithm is a step-by-step set of instructions used to solve a problem or perform a task. It can be iterative (repeating steps) or recursive (where a function calls itself).
Example: Following a recipe to bake a cake is an algorithm. It tells you step-by-step what to do. Each step leads you closer to the final goal.
Fractals
Fractals are complex, self-repeating patterns that look the same no matter how much you zoom in or out. They are formed using iterative processes.
Example: Snowflakes are natural examples of fractals. No matter how much you zoom in on a snowflake, the pattern looks similar at every level. The same repeating shape/pattern appear as you zoom in closer, showing the fractal property.
Diagrams and Their Uses
Diagrams help us visualize ideas, processes, and relationships in an easy-to-understand way. Here are some common types:
Arrow Diagrams
Arrow diagrams are used to show movement or direction, often in processes where one step leads to another. The arrows make it clear what happens first, next, and last.
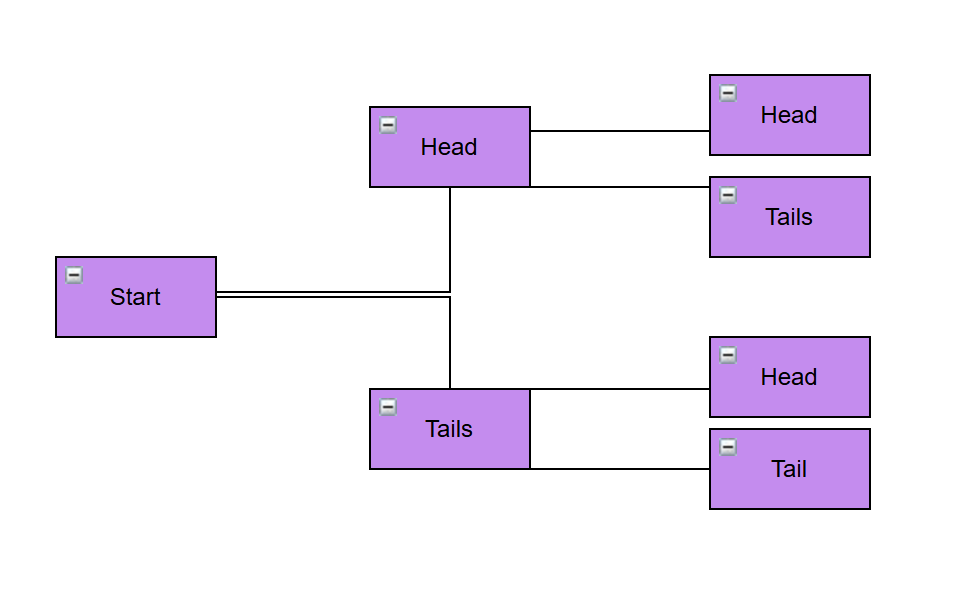
Tree Diagrams
Tree diagrams help show how things branch out from one starting point. They are often used to show choices, classifications, or family relationships.
Recursive Functions
A recursive function will call itself repeatedly with smaller sub-problems until it reaches a base case. A recursive formula is a way of defining a sequence (a list of numbers) where each term is based on the one before it. It can be expressed algebraically as such:
This formula helps us find the next number in a sequence by using the two numbers before it. To get the next number, you take the one right before it, multiply it by 3, and then subtract the number two steps before it. It’s like following a pattern where each new number depends on the ones that came before it. So, you start with a couple of known numbers, and you can keep using the formula to find more numbers in the sequence.
Example
Given the first two terms: \( t_0 = 2 \) and \( t_1 = 5 \), use the recursive formula \( t_n = 3t_{n-1} - t_{n-2} \) to calculate the next three terms.
First, we can calculate \(t_2\):
\( t_2 = 3t_1 - t_0\)
\( 3t_2 = 3(5) - 2\)
\(t_2 = 13\)
Next, we can calculate \( t_3 \):
\( t_3 = 3t_2 - t_1\)
\(t_3 =3(13) - 5\)
\(t_3 = 34\)
Then, we can calculate \( t_4 \):
\( t_4 = 3t_3 - t_2\)
\(t_4= 3(34) - 13\)
\(t_4 = 89\)
Therefore, we can determine that the next three terms in the sequence are 13, 34, and 89.
We can write the sequence thus far as such:
An iterative process involves repeating steps over and over until a task is complete. An algorithm is a step-by-step set of instructions used to solve a problem. Some algorithms are iterative (using loops to repeat steps), while others are recursive (where a function calls itself with smaller subproblems until reaching a base case). For example, cleaning a room involves iterations, while following a recipe is an algorithm that can be either iterative or recursive.
Fractals are special patterns that look the same no matter how much you zoom in or out. They are formed using iterative processes, meaning they repeat a pattern at different scales. A fractal diagram shows this self-repeating nature, like the Sierpinski Triangle, where smaller triangles repeat inside a larger one. Fractals appear in nature, such as in snowflakes and tree branches.
Recursive functions solve problems by breaking them into smaller versions of themselves until reaching a base case. A tree diagram represents recursion well because it branches into smaller subproblems. A real-life example is a nesting doll, where each doll contains a smaller one inside. To see all dolls, you open one, then the next, repeating the process until you reach the smallest doll. Just like recursion breaking a problem into smaller parts.