Radiative Decay
When a nuclide is unstable (radioactive) is can decay by various nuclear processes to a lower (stable) energy state. Each nuclide randomly decays following a poisson distribution at a decay rate \(\lambda\). Since there is a very large number of individual nuclides, we can calculate the average number remaining. Let's assume a radioactive substance decays into a stable daughter element:
\(A^* \rightarrow B\)
The number of radioactive nuclides is \(N\) and decreases with time as they decay into the daughter nuclude. Thus, \(N = N(t)\). The rate of change is \(\frac{dN}{dt} = -\lambda \cdot N \) since the quantity decreases at a constant rate and is proportional to the amount of radioactive nuclides available to decay. Solving the differential equation yields:
\(\cfrac{dN}{dt} = -\lambda \cdot N \)
\(\int\cfrac{dN}{N} = \int-\lambda \cdot dt \)
\(\ln(N) = -\lambda \cdot t + C\)
\(N(t) = e^{-\lambda \cdot t + C}\)
\(N(t) = e^{-\lambda \cdot t} \cdot e^{C}\)
\(N(t) = e^{-\lambda \cdot t} \cdot C^{'}\)
The initial boundary condition is \(N(t=0)=N_0\). At \(t = 0\) we have the initial amount of radioactive nucludes \(N_0\):
\( N(t) = e^{-\lambda \cdot t} \cdot C^{'}\)
\( N(0)=N_0 = e^{-\lambda \cdot (0)} \cdot C^{'}\)
\( N_0 = C^{'}\)
This gives the final equation describing the exponential decay of a radioactive element:
\(N(t) = N_0 \cdot e^{-\lambda \cdot t}\)
There are still \(N_0\) total nuclide after some time passes but some are now daughter atoms. The number of daughter atoms increases with time:
\(N_D(t) = N_0 - N(t) \)
\(N_D(t) = N_0 - N_0 \cdot e^{-\lambda \cdot t} \)
The relationship between parent and daughter nuclides is shown below:
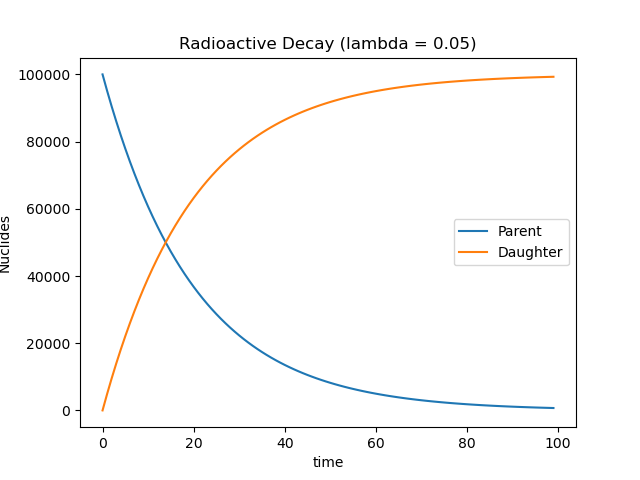
A radioactive sample (\(10 \; [\text{g}]\)) decays for \(5 \; [\text{hr}]\). Your lab partner calculates that \(3 \; [\text{g}]\) of radioactive material remains. What is the mass of the stable nuclide?
At all times, unless a gust of wind takes some of your sample, there is \(10 \; [\text{g}]\) of parent + daughter. Assuming the radioactive element decays to a stable daughter, the mass is:
\(N_D(t) = N_0 - N(t) \)
\(N_D(t) = 10 - 3 \)
\(N_D(t) = 7 \; [\text{g}] \)
Therefore, we can determine there is roughly \(\boldsymbol{7 \; [\textbf{g}]}\) of the stable daughter nuclide.
Review these lessons:
Try these questions:
Half-Life
A common quantity in radioactive decay is the half-life. The half-life is the amount of time it takes for half the radioactive substance to decay. After \(2\) half-lives, \(25 \%\) of the substance remains and so on. After about \(5\) half-lives, the radioactive material has mostly decayed.
| # Half-Lives | Radioactive Material (%) | Stable Material (%) |
| \(1\) | \(50\) | \(50\) |
| \(2\) | \(25\) | \(75\) |
| \(3\) | \(12.5\) | \(87.5\) |
| \(4\) | \(6.25\) | \(93.75\) |
| \(5\) | \(3.125\) | \(96.875\) |
We can express the formula above in terms of the half-life, \(t_{1/2}\), accordingly:
\(N(t) = N_0 \cdot e^{-\lambda \cdot t} \)
\(N(t_{1/2})= \cfrac{N_0}{2} = N_0 \cdot e^{-\lambda \cdot t_{1/2}} \)
\(\cfrac{N_0}{2} = N_0 \cdot e^{-\lambda \cdot t_{1/2}} \)
\(\cfrac{1}{2} = e^{-\lambda \cdot t_{1/2}} \)
\(-\ln\left(\cfrac{1}{2}\right) = -\lambda \cdot t_{1/2} \)
\(\cfrac{-\ln \left(\frac{1}{2}\right)}{\lambda} = t_{1/2} \)
\(t_{1/2} = \cfrac{\ln(2)}{\lambda}\)
\(\lambda = \cfrac{\ln(2)}{t_{1/2}}\)
\(N(t) = N_0 \cdot e^{-ln(2) \cfrac{t}{t_{1/2}}} \)
A radioactive element has a half-life of \(A \; [\text{mins}]\). If the daughter element is stable, what percentage exists after \(3\) half-lives.
We do not need to know the actual value of the half-life since we know \(t = 3t_{1/2}\).
First, we can determine the quantity of the element after \(3\) half-lives as such:
\(N(t) = N_0 \cdot e^{-ln(2) \frac{t}{t_{1/2}}} \)
\(N(3t_{1/2}) = N_0 \cdot e^{-ln(2) \frac{3t_{1/2}}{t_{1/2}}} \)
\(N(3t_{1/2}) = N_0 \cdot e^{-3ln(2)} \)
\(N(3t_{1/2}) = N_0 \cdot e^{ln(2^{-3})} \)
\(N(3t_{1/2}) = N_0 \cdot 2^{-3} \)
Next, we can determine the amount of daughter nuclides as such:
\( N_D(3t_{1/2}) = N_0 - N(3t_{1/2}) \)
\( N_D(3t_{1/2}) = N_0 - N_0 \cdot 2^{-3} \)
\( N_D(3t_{1/2}) = N_0 (1 - 2^{-3} )\)
\( N_D(3t_{1/2}) = 0.875N_0\)
Thererfore, we can determine \(87.5 \%\) of the original sample has decayed to the daughter nuclide. This means \(\boldsymbol{12.5 \%}\) remains radioactive since the total is \(100 \%\). These results are consistent with the table above.