Piecewise Functions
Piecewise Functions are functions that are made up of different mathematical expressions or rules for different intervals within its domain. In other words, they are smaller functions that contain different pieces that make up a larger function.
Here is a basic formula for piecewise functions:
\[ f(x) = \begin{cases} f_1(x) & \text{if } \text{condition}_1 \\ f_2(x) & \text{if } \text{condition}_2 \\ \vdots \\ f_n(x) & \text{if } \text{condition}_n \\ g(x) & \text{otherwise} \end{cases} \]
The function is broken up into separate parts. There will be multiple individual smaller functions (pieces) with a restriction of where they will be represented on the domain.
Example
Sketch the following piecewise function:
\[ f(x) = \begin{cases} x^2 & \text{if } x \leq 0 \\ 2x + 1 & \text{if } x > 0 \end{cases} \]
In this example, \(f(x)=x^2\) will be represented when the \(x\) value (domain) is smaller to or equal to 0, and \(f(x)=2x+1\) will be represented when the \(x\) value is larger than \(0\). The function is graphed below:
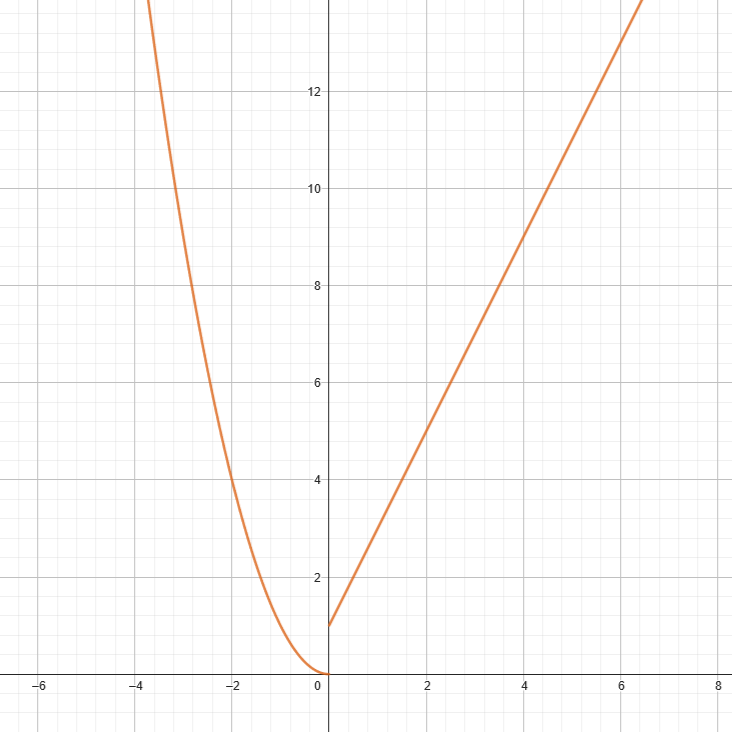
One important rule to remember is that each piece of a piecewise function should not over lap. In this case, the domain of \(x^2\) is \(0\) and everything less than \(0\), whereas for \(2x+1\), the domain is everything above \(0\), not including \(0\) itself.
Example
Sketch the following piecewise function:
\[ f(x) = \begin{cases} 2x & \text{if } x < -1 \\ x & \text{if } -1 \leq x < 0 \\ x^2 & \text{if } 0 \leq x < 1 \\ \frac{1}{x} & \text{if } x \geq 1 \end{cases} \]
\(2x\) will be represented when the domain is less than \(-1\), \(x\) will be represented when the domain is \(-1 \leq x < 0\), \(x^2\) will be represented when \(0 \leq x < 1\), and \(\frac{1}{x}\) will be represented when the domain is equal to or greater than \(1\). Here is the graphed function:
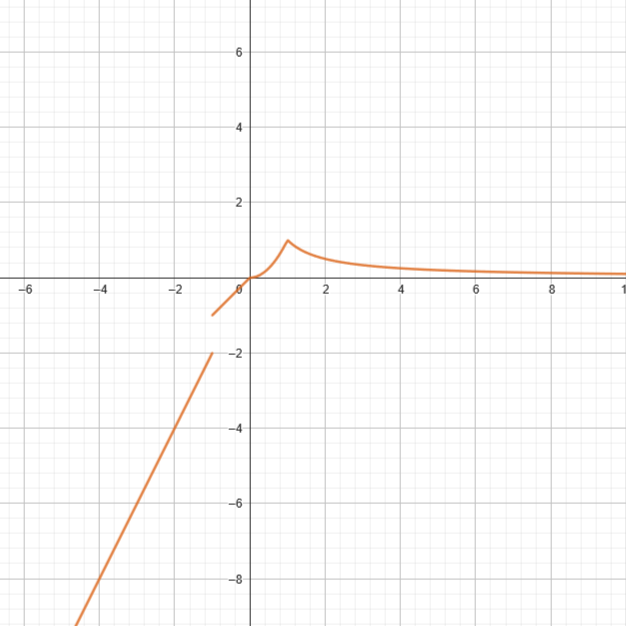
As you can see, each individual piece is easily distinguishable and there is no overlap of domains.
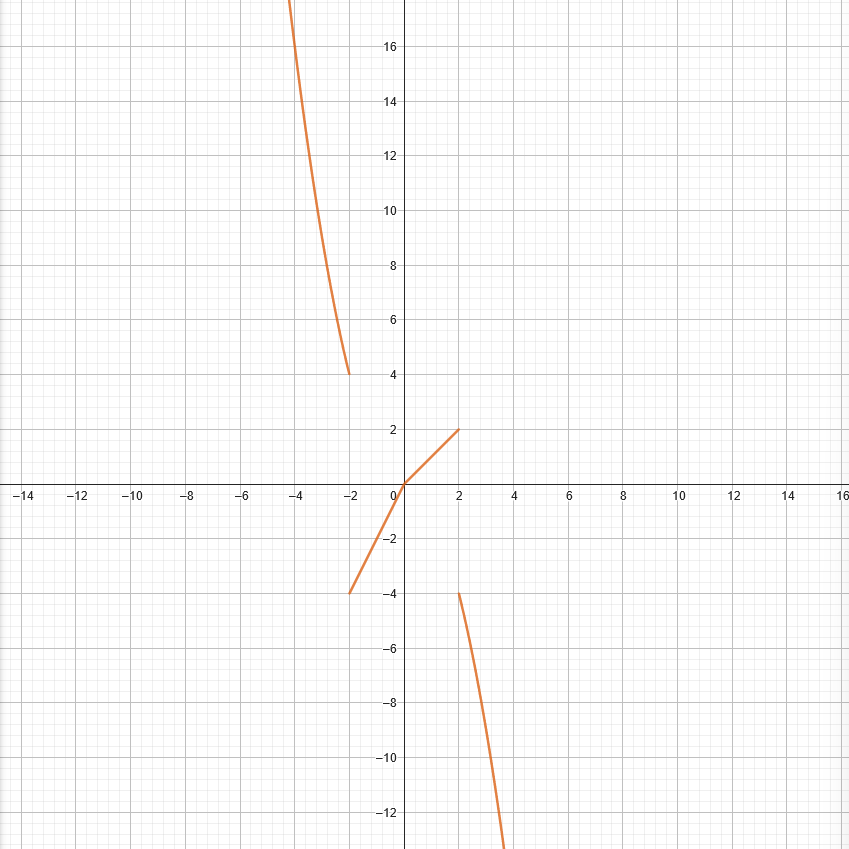
\[ f(x) = \begin{cases} x^2 & \text{if } x < -2 \\ 2x & \text{if } -2 \leq x < 0 \\ x & \text{if } 0 \leq x < 2 \\ -x^2 & \text{if } x \geq 2 \end{cases} \]
\(x^2\) will be represented when the domain is less than \(2\), \(2x\) will be represented when the domain is \(-2 \leq x < 0 \), \(x\) will be represented when that domain is \(0 \leq x < 2\), and \(-x^2\) will be represented when the domain is equal or greater than \(2\).
Here is the graphed result:
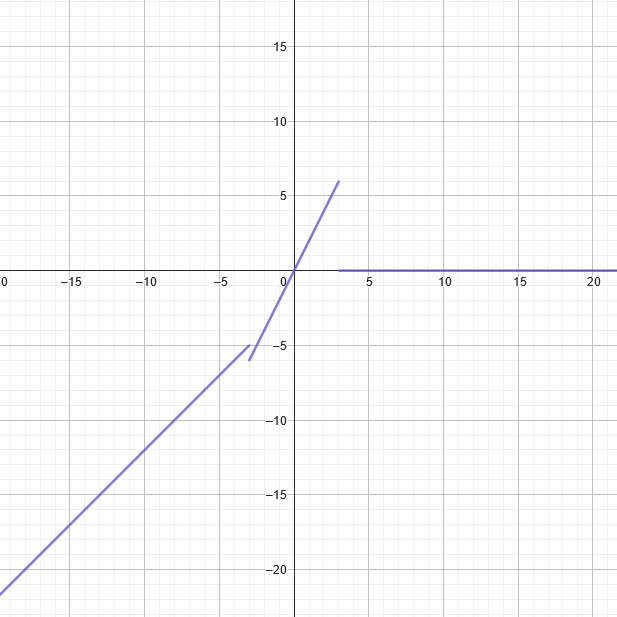
\[f(x) = \begin{cases} x - 2 & \text{if } x < -3 \\ 2x & \text{if } -3 \leq x \leq 3 \\ 0 & \text{if } x > 3 \end{cases} \]
\(x- 2\) will be represented when the domain is less than \(-3\), \(2x\) will be represented when the domain is \(-3 \leq x \leq 3\), and \(0\) will be represented when the domain is greater than \(3\).
Here is the graphed result: