Logarithmic Functions

Logarithmic Functions are functions that represent the inverse of exponential functions. They are algebraically expressed as such:

\(f(x)=\log_b(x)\)

Understanding logarithmic functions is useful for solving problems involving exponential relationships. Since inverses are reflections about the line \(f(x)=x\), the logarithmic function of its exponential counterpart will be a symmetrical reflection on the other side of \(y=x\). Additionally, the base of the logarithmic function should never be negative.

By having the table of values for an exponential function, it is very easy to find and plot the points for its logarithmic counterpart.

Here's an example of the exponential function, \(f(x)=2^x\) and a partial table of values:

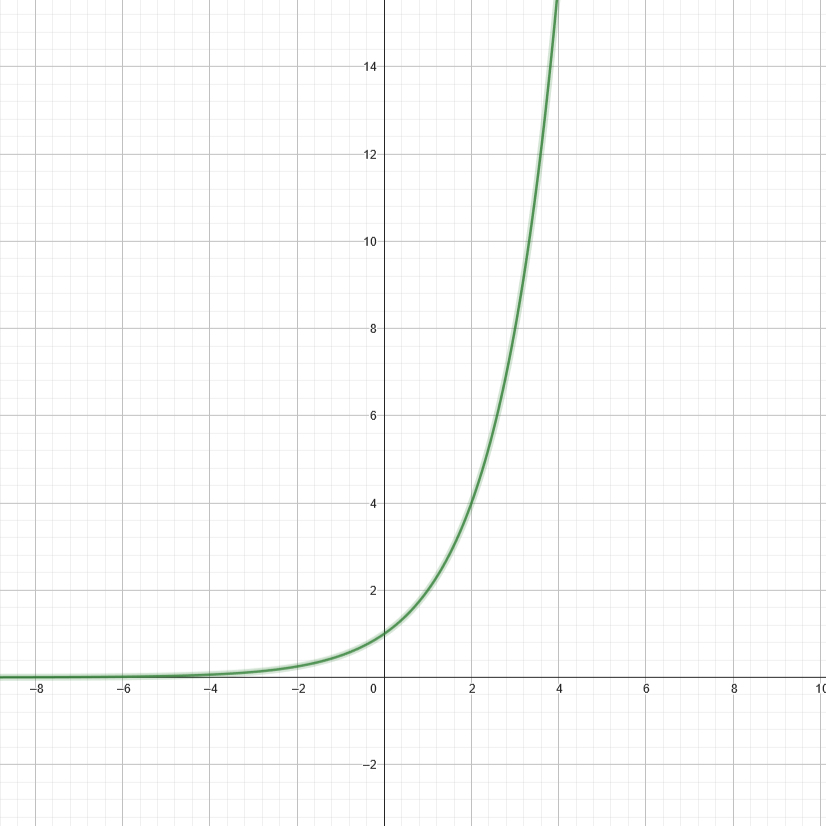
\(\boldsymbol{x}\)	\(\boldsymbol{2^x}\)
\(-2\)	\(\cfrac{1}{4}\)
\(-1\)	\(\cfrac{1}{2}\)
\(0\)	\(1\)
\(1\)	\(2\)
\(2\)	\(4\)
\(3\)	\(8\)

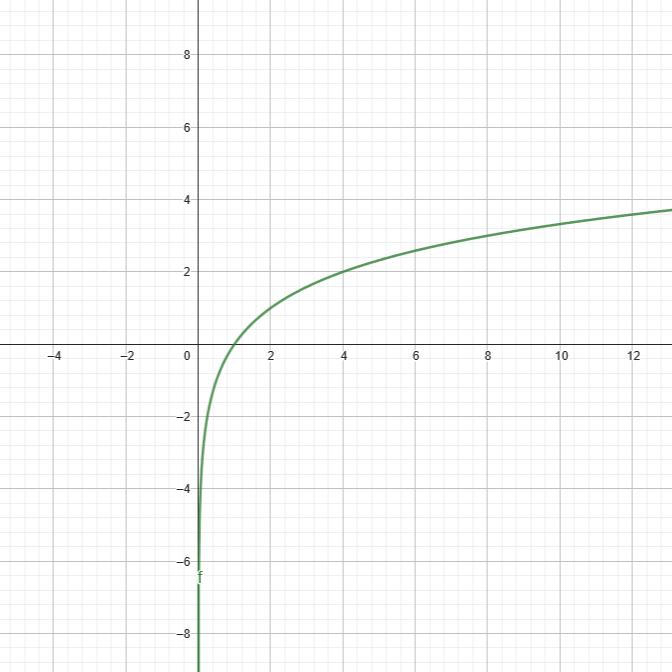
To find the logarithmic inverse of \(f(x)=2^x\), the logarithmic formula must be used, \(g(x)= \log_2(x)\). Since this is the inverse, constructing the table of values just requires flipping the values of the exponential function table of values. The logarithmic table of values in shown below:

\(\boldsymbol{x}\)	\(\boldsymbol{\log_2(x)}\)
\(\cfrac{1}{4}\)	\(-2\)
\(\cfrac{1}{2}\)	\(-1\)
\(1\)	\(0\)
\(2\)	\(1\)
\(4\)	\(2\)
\(8\)	\(3\)

When those points get plotted on the graph, it will look something like this:

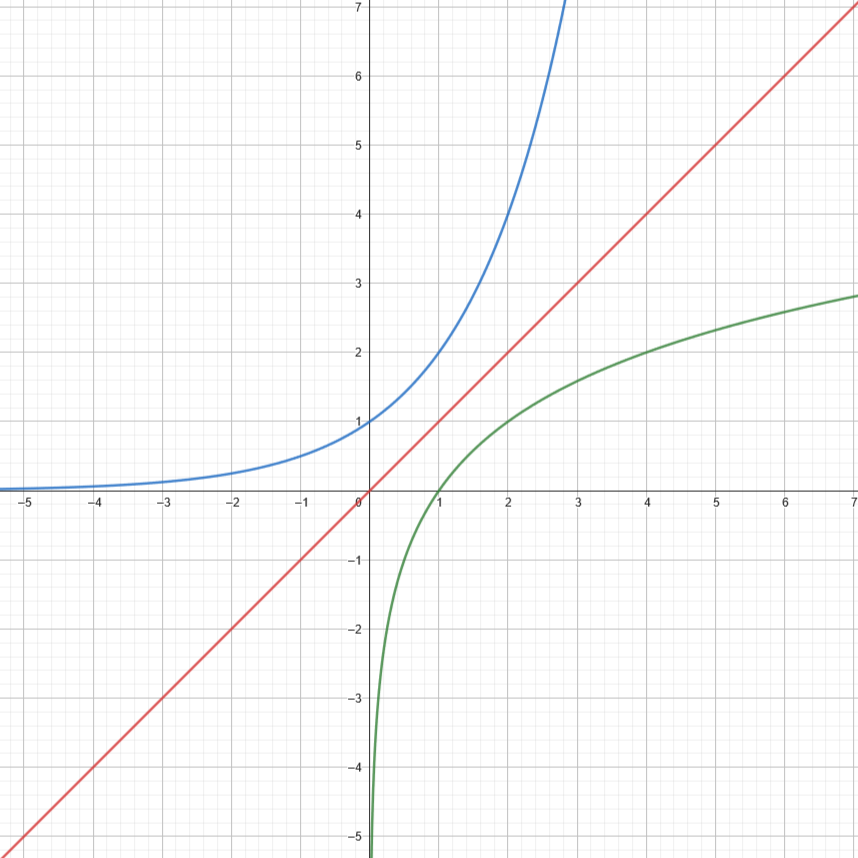
Now, lets see what both functions look like on a graph with the line of reflection:

Exponential and Logarithmic functions with a base between \(0\) and \(1\) have a slightly different behaviour to them. Represented below are the functions, \(d(x)=\frac{1}{2}^x\) and \(w(x)=\log_\frac{1}{2}(x)\):

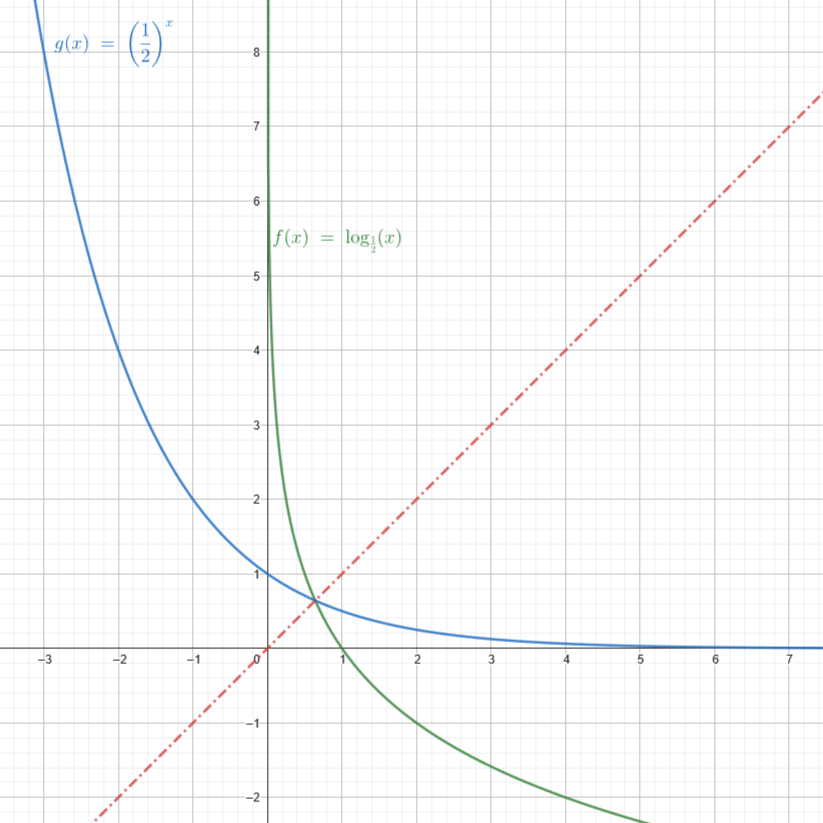
As you may have noticed, the functions cross eachother and have slightly different behaviours than functions with a base that's atleast 1. Also, these two functions are still symmetrical to eachother at \(y=x\).

---