Geometry
To understand more about triangular geometry, we have to learn a few more terms.
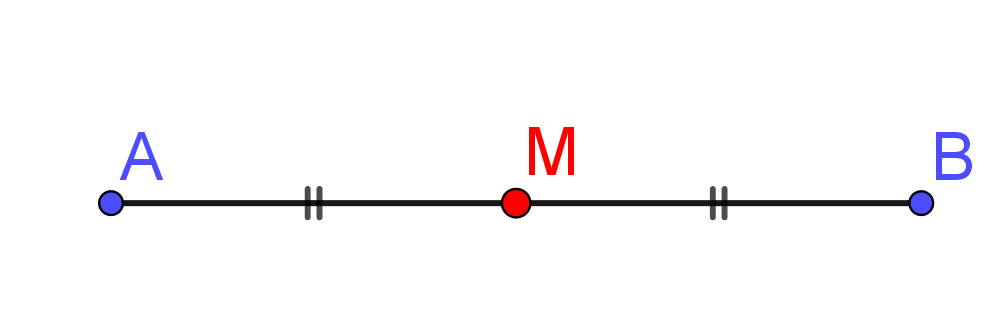
Midpoint
The Midpoint of a segment is the point that divides the segment into two congruent (identical) segments.
We can find the midpoint of a line using the following formula:
\((x_m,y_m) = \left(\cfrac{x_2+x_1}{2}, \cfrac{y_2+y_1}{2}\right)\)
Median
A Median is a line segment that extends from the vertex (corner) of one side of the triangle to the midpoint of the other side.
We can find the length of the median using the following formula:
\(m_a = \sqrt{\cfrac{2b^2 + 2c^2 - a^2}{4}}\)

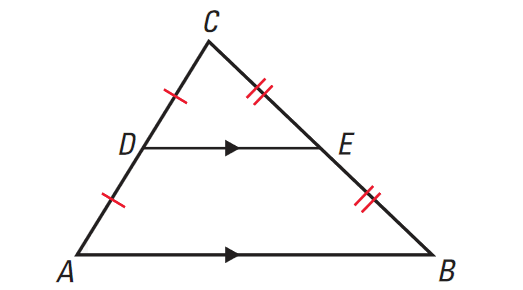
Midsegment
A Midsegment is a line segment connecting the midpoints of two sides of a triangle. it is also parallel to the third side of the triangle and is half of the length of the third side!
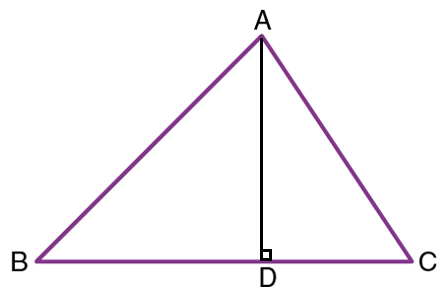
Altitude
An Altitude is a line segment that extends from the vertex (corner) of one side of the triangle and is perpendicular to the opposite line segment.
Perpendicular Bisector
The Perpendicular Bisector is a line or a segment perpendicular to a segment that passes through the midpoint of the segment. Then, the perpendicular bisector of a side of a triangle would be a line perpendicular to the side and passing through its midpoint. Since there are three perpendicular bisectors on the sides of a triangle, and they meet in a single point, that point would be called the circumcenter. The three perpendicular bisector of the triangle would converge at the center of the red circle.

Angle Bisector
The Angle Bisector of an angle of a triangle would be a straight line that divides the angle into two congruent (equal) angles. Since there are three angle bisectors on the sides of a triangle, and they meet in a single point, that point would be called the incenter.

Centroid
The Centroid is the central point of the triangle which the 3 medians cross over. The centroid lies two-thirds of the distance from each vertex to the midpoint on its opposite side.
We can find the median of a line using the following formula:
\(\text{Centroid} = \left[\cfrac{x_1 + x_2 + x_3}{3}, \cfrac{y_1 + y_2 + y_3}{3} \right]\)
The line is drawn from a vertex of a triangle to the midpoint of the opposide side. The line is a median. There is not enough information to determine if the line is also an altitude or angle bisector.
Both median and altitudes are drawn from the vertex. However, a median is drawn to the midpoint of the opposite side where as an altitude is perpendicular to the opposite side.
To find the midpoint of these two points, we can plug the coordinate values into the midpoint formula and simplify:
\((x_m,y_m) = \left(\cfrac{x_2+x_1}{2}, \cfrac{y_2+y_1}{2}\right)\)
\((x_m,y_m) = \left(\cfrac{5+1}{2}, \cfrac{-5+y_5}{2}\right)\)
\((x_m,y_m) = \left(\cfrac{6}{2}, \cfrac{0}{2}\right)\)
\((x_m,y_m) = (3, 0)\)
Therefore, we can determine that the midpoint is located at \(\boldsymbol{(3,0)}\).