Angles
Angles represent the space between two lines (measured in degrees). Let's take a look at different types of angles:
| Type | Description |
|---|---|
| Acute Angle | it is less than \(90°\) |
| Right Angle | it is exactly \(90°\) |
| Obtuse Angle | it is greater than \(90°\) but less than \(180°\) |
| Straight Angle | it is exactly \(180°\) |
| Reflex Angle | it is greater than \(180°\) but less than \(360°\) |
| Full Rotation | it is \(360°\) exactly |
Review these lessons:
Try these questions:
Opposite Angles
Opposite Angles are across the transversal. Opposite angles are equal to each other.

Corresponding Angles
Corresponding Angles are in the same position relative to lines intersected by a transversal. Corresponding angles are equal when the two lines intersected by the transversal are parallel.

Alternate Angles
Alternate Angles are in opposite positions relative to a transversal intersecting two lines. Alternate angles are equal when the two lines intersected by the transversal are parallel.

Co-Interior Angles
Co-Interior Angles are on the same side of an transversal line when it intersect two other lines. Co-interior angles add to \(180^\circ\).

Supplementary Angles
Two angles are supplementary when they add up to \(180^{\circ}\) (they make a straight line).
\(\angle A\) and \(\angle B\) below form a straight line so they must add to \(180^{\circ}\).
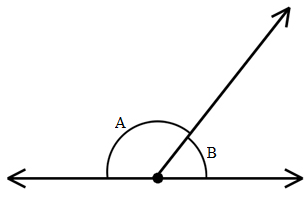
Complementary Angles
Two angles are complementary when they add up to \(90^{\circ}\) (a right angle).
\(\angle{\text{DAC}}\) and \(\angle{\text{CAB}}\) form a right angle and would add up to \(90^{\circ}\).

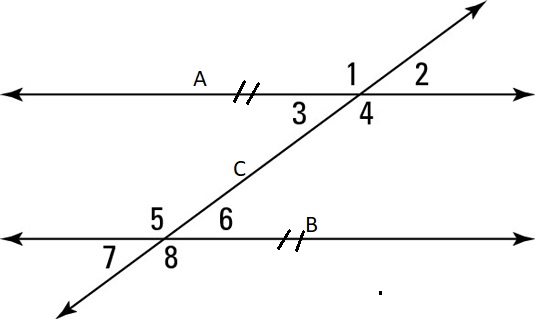
Refer to the figure below. Guess which angles correspond with each type then press the button to show the answer.
Line C is the transversal line.
Line A and line B are the parallel lines.
\(\angle 1 \ \&\ \angle4\), \(\angle 3 \ \&\ \angle 2\), \(\angle 5 \ \&\ \angle 8\) and \(\angle 6 \ \&\ \angle 7\) are opposite angles.
\(\angle 1 \ \&\ \angle 5\), \(\angle 3 \ \&\ \angle 7\), \(\angle 2 \ \&\ \angle 6\) and \(\angle 4 \ \&\ \angle 8\) are corresponding angles.
\(\angle 3 \ \&\ \angle 6 \) and \( \angle 4 \ \&\ \angle 5\) are alternate angles.
\(\angle 3 \ \&\ \angle 5 \) and \( 4 \ \&\ \angle 6\) are co-interior angles.
\(\angle 1 \ \&\ \angle 2\), \(\angle 3 \ \&\ \angle 4\), \(\angle 5 \ \&\ \angle 6\), \(\angle 7 \ \&\angle 8\), \(\angle 1 \ \&\ \angle 3\), \(\angle 2 \ \&\ \angle 4\), \(\angle 5 \ \&\ \angle 7\) and \(\angle 6 \ \&\ \angle 8\) are supplementary angles.
There are no complementary angles.
Let us assume that \(x\) represents the supplementary angle. Since supplementary angles must add to \(180^\circ\), we can isolate for \(x\) to determine its value:
\(40 + x = 180\)
\(x = 140\)
Therefore, we can determine that \(\boldsymbol{140^\circ}\) is supplementary to \(40^\circ\).
Let us assume that the smaller angle = \(x\), then the larger angle = \(2x\). Since they are complementary, they add up to \(90^\circ\):
\(x + 2x = 90\)
\(3x = 90\)
\(x = 30^\circ\)
With \(x\) solved, we can now determine the value of the larger angle:
\(\theta = 2(30^\circ)\)
\(\theta = 60^\circ\)
Therefore, we can determine the value of the larger angle is \(\boldsymbol{60^\circ}\).
The \(10\) angles would be supplementary and add up to \(180^\circ\). Since they are equal, we can say each is equal to \(x\):
\(10x = 180\)
We can now divide both sides by \(10\) to determine the value of each individual angle:
\(10x = 180\)
\(x = 18\)
Therefore, we can determine that each angle is \(\boldsymbol{18^\circ}\).